Processing
14. ベジエ曲線を利用する
ベジエ曲線は、直線や円弧とは異なる複雑な図形の描画も可能です。
指定する座標が多く、また描かれる曲線の姿が想像しにくい面もありますが、上手く利用すると多様な表情の図形を描くことができます。
制御点を規則的に変化させる
void setup() {
size( 500, 500 );
background( 255 );
smooth();
noLoop();
rectMode( CENTER );
}
void draw() {
int leftX = 50; //始点のx座標
int topY = 50; //始点のy座標
int rightX = 450; //終点のx座標
int bottomY = 450; //終点のy座標
int repeatNum = 50; //繰返しの回数
float controlPitch = ( rightX - leftX ) / repeatNum; //制御点を移動させる幅を、横幅を繰返しの回数で割って求める
int controlSpan = 100;
stroke( 204, 51, 0 );
noFill();
for( int i = 0; i < repeatNum; i++ ) {
float controlX = leftX + i * controlPitch;
float controlY = bottomY - i * controlPitch;
bezier( leftX, topY,
controlX, controlY - controlSpan,
controlX, controlY + controlSpan,
rightX, bottomY );
//rect( controlX, controlY - controlSpan, 4, 4 );
//rect( controlX, controlY + controlSpan, 4, 4 );
}
}
ベジエ曲線を練習する時、始点や終点、制御点を規則的に変化させると、どのような性質を持った曲線なのかが理解しやすくなります。
26行目〜29行目、長くなるので改行していますが、1行に書いても同じことです。
26行目、ベジエ曲線の始点は、x座標leftX、y座標topYに固定です。29行目、ベジエ曲線の描き終わりもx座標rightX、y座標bottomYに固定です。
24、25行目で、ベジエ曲線の2つの制御点の座標の基準を計算で求めていますが、画面左下から画面右上に等間隔で変化するようにしています。
27、28行目、21、22行目で求めた点から実際の制御点の位置を、y方向に-controlSpan、+ controlSpanしています。つまり上下に100ピクセルずらしています。
制御点の間隔は、描画全体の幅( rightX - leftX )を繰返しの回数で割って求めていますので、repeatNumの値さえ変えればベジエ曲線の本数を変えることができます。
30、31行目をコメントではなくすると、制御点の位置に小さな四角が描かれます。

ベジエ曲線は、始点、終点、制御点を変えると、ちょっとした変更でも大きくその表情を変えます。色々試してみて欲しいと思います。
void setup() {
size( 500, 500 );
background( 255 );
smooth();
noLoop();
rectMode( CENTER );
}
void draw() {
int leftX = 50; //始点のx座標
int topY = 50; //始点のy座標
int rightX = 450; //終点のx座標
int bottomY = 450; //終点のy座標
int repeatNum = 50; //繰返しの回数
float controlPitch = ( rightX - leftX ) / repeatNum; //制御点を移動させる幅を、横幅を繰返しの回数で割って求める
stroke( 204, 51, 0 );
noFill();
for( int i = 0; i < repeatNum; i++ ) {
float controlX1 = leftX + i * controlPitch;
float controlX2 = rightX - i * controlPitch;
bezier( controlX1, topY,
controlX1, 1000,
controlX2, -500,
controlX2, bottomY );
}
}

ベジエ曲線を描画単位に利用する
「13. 描画の単位を考える」で行ったような描画単位にベジエ曲線を利用してみます。
どのような描画単位しようか考える際には、いきなり数多くの繰返しを行うのではなく(例えば以下のrepeatNumを1にしておくなどして)描画単位がある程度作り、その上で繰返しを行った方が良いでしょう。
描画単位:異なる大きさの波形の線
void setup() {
size( 500, 500 );
background( 255 );
smooth();
noLoop();
colorMode( HSB, 360, 100, 100, 100 );
}
void draw() {
int repeatNum = 9;
int shapePitch = 50;
int shapeSize = 50;
int pitchWidth = shapePitch * ( repeatNum - 1 );
int leftX = ( width - pitchWidth ) / 2;
for( int i = 0; i < repeatNum; i++ ) {
for( int j = 0; j < repeatNum; j++ ) {
float drawPointX = leftX + j * shapePitch;
float drawPointY = leftX + i * shapePitch;
float lineAlpha = random( 50, 100 );
stroke( 240, 80, 70, lineAlpha );
strokeWeight( random( 1, 4 ) );
noFill();
drawShape( drawPointX, drawPointY, shapeSize );
}
}
}
void drawShape( float centerX, float centerY, int drawSize ) {
int repeatBezNum = 5;
float ctlPointPitch = drawSize / repeatBezNum;
float preX = centerX - drawSize / 2;
for( int i = 0; i < repeatBezNum; i++ ) {
float yuragiX = random( -ctlPointPitch/4, ctlPointPitch/4 );
float yuragiY1 = random( drawSize, drawSize*3 );
float yuragiY2 = random( drawSize, drawSize*3 );
float postX = preX + ctlPointPitch;
bezier( preX, centerY,
postX - ctlPointPitch/2 - yuragiX, centerY - yuragiY1,
postX - ctlPointPitch/2 + yuragiX, centerY + yuragiY2,
postX, centerY );
preX = postX;
}
}
23、24行目、繰返しの中で線の透明度に指定する変数の値をランダムに求め、色の透明度を変えています。同様に、25行目、線の太さもランダムにしています。
40〜50行目、drawShape()内で、さらに繰返しを記述し、その回数に応じて波の形になるように、ベジエ曲線に必要な座標を変化させています。
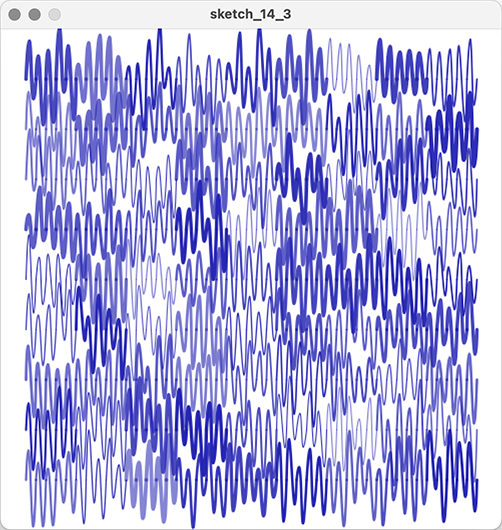
ランダムを多用すれば良いというものでもないのですが、プログラムで手描きらしさをどのように出すか、ということも考えてみる方向の1つとしては面白いかもしれません。
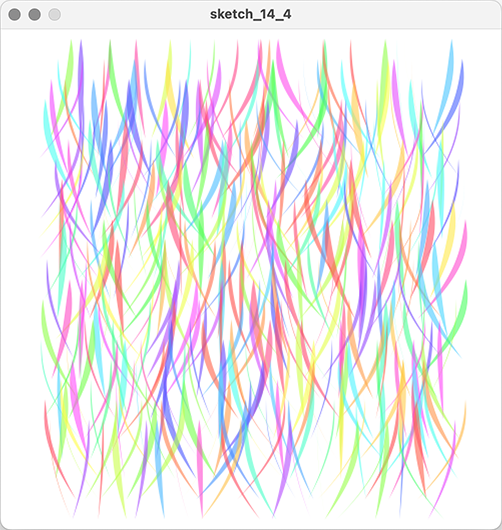
描画単位:ベジエ曲線でつくる形
void setup() {
size( 500, 500 );
background( 255 );
smooth();
noLoop();
colorMode( HSB, 360, 100, 100, 100 );
}
void draw() {
int repeatNum = 20;
int shapePitch = 20;
int shapeSize = 100;
int pitchWidth = shapePitch * ( repeatNum - 1 );
int leftX = ( width - pitchWidth ) / 2;
for( int i = 0; i < repeatNum; i++ ) {
for( int j = 0; j < repeatNum; j++ ) {
float drawPointX = leftX + j * shapePitch;
float drawPointY = leftX + i * shapePitch;
float colorHue = random( 360 );
fill( colorHue, 70, 100, 60 );
noStroke();
drawShape( drawPointX, drawPointY, shapeSize );
}
}
}
void drawShape( float centerX, float centerY, int drawSize ) {
float tmpX = random( -drawSize/4, drawSize/4 );
float yuragiX = random( 5 );
float topX = centerX + tmpX;
float bottomX = centerX - tmpX;
beginShape();
vertex( topX, centerY - drawSize/2 );
bezierVertex( topX + yuragiX, centerY - drawSize/4,
topX + yuragiX, centerY,
bottomX, centerY + drawSize/2 );
bezierVertex( topX - yuragiX, centerY,
topX - yuragiX, centerY - drawSize/4,
topX, centerY - drawSize/2 );
endShape();
}
ベジエ曲線で形を描く場合、40行目、beginShape();で始め、48行目、endShape();で終わります。
41行目、図形の始点へvertex()を使って移動し、その後はbezierVertex()で図形を描きます。
bezierVertex()は直前の描画の終点がそのまま始点になります。
つまり45行目の時点では、直前のベジエ曲線の終点の座標が、自動的に次の曲線の始点になります。したがって、bezierVertex()をつなげて書くことで、ベジエ曲線で囲まれた図形を描くことができます。