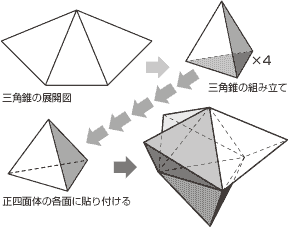
ギリシャ時代には火・地・空気・水など宇宙を構成するとして、5つの正多面体（正四面体・正六面体・正八面体・正十二面体・正二十面体）が既に発見され、正多面体はこの5つしかなく、正二十面体以上の正多面体がないことも解っていた。
　正三角形は6つ集まると平面ができるが、5枚以下で貼り合わせれば立体になる。正方形（4枚）と正五角形（5枚）が正多角形を構成する正多角形です。
　多面体はこの正多面体を基本として発展し、その応用形態にはたくさんの種類や造形的な可能性がある。
　正多面体の展開図はそれぞれ1つではない。ここに掲載したもの以外にもあるので使いやすいものを選択する。
　4枚の正三角形を組み合わせて構成されている。正三角錐とも呼ぶ。
　正方形、6枚で構成されている。立方体の別称である。全部で11種類の展開図の取り方がある。辺の長さだけでなく、すべての角は90°でこれも等しい。面や辺どうしは3方向で平行になる。
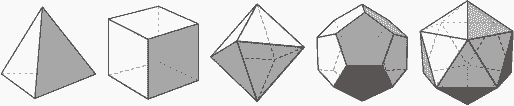
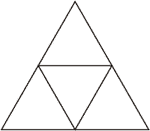
正四面体の展開図
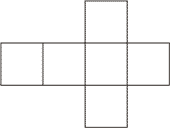
正六面体の展開図
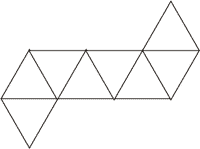
　正三角形、8枚による正多角形。ピラミッドのように正方形を底面とする正四角錐を2つ合わせた形。
正八面体の展開図
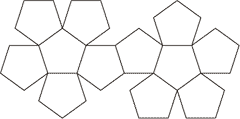
　正五角形12枚によって構成される正多面体。希にサッカーボールの展開図と同じと間違えている人がいるが、サッカーボールは正六角形との組み合わせでできている。
　正三角形20枚によって構成される正多面体。かなり、球に近づいてくる。
正十二面体の展開図
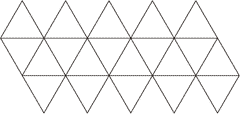
正二十面体の展開図
　正多面体が正三角形と正方形、正五角形でできているなら、それらを底面として考え、色々な多面体を作り各面に貼り付けていくと、複雑な多面体の応用立体ができあがる。
　正多角形の各面を膨らませるだけでなく、穴を開けたり、各面をその他の加工を加えながら正多面体の構造に合わせると、更にたくさんの多面体応用立体を作ることができる。
　しかし複雑な形態になる程、1枚の紙で展開図を取ることができなくなる。そこで「パーツ分け」と考え、パーツごとに色を変えたり、ジョイント方法を工夫するとより面白い展開が広がっていき、パッケージデザインなどに応用できる。
　底面が正三角形になる三角錐を作り、正四面体の各面に貼り付けると全く違った多面体ができます。