線分と角の等分・正多角形の作図
　平面製図の中でも線分・角・正多角形の作図を掲載し、基本的な製図を取り上げ説明する。
　線分の両端A、Bから同じ半径の弧を描き、それぞれの交点を結べば線分の「垂直2等分線」を引くことができる。
　線分aの両端をA、Bとし、Aから補助線ACを任意に取る。AC上に点Aより順次Aｎ個の等倍点を取っていく。点Anと点Bを結び、その線と平行に点A1〜Anまで、各点を通る線を引いていくと、線分ABとの交点が求める等分点になる。
　線分ABと線分CDを半径ｒでつなぐ時、まず、交点Eから半径ｒの弧を引き、Eから等距離の点F,Gを取る。F,Gから同じく半径ｒで弧を引き交点Oを求める。この交点Oが求めるこの中心点になるので線分をつなぐように製図する。
　ただし、この製図法では、弧と線分とののつなぎ目がへこんで見える。これを回避するためには接点の少し手前で半径より大きな弧でつないでへこみ感を解消する。視覚的に自然な見え方を求める描画方法である。
　AOBで、Oを中心に弧を描き、AO、OBとの交点C、Dを求める。
　次にC、Dから同じ半径の弧を描き、2つの交点を求める。その交点とOとを結べば角AOBを2等分することができる。
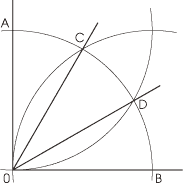
　角の3等分は任意の角ではできないが、直角だけは3等分することが可能である。
　AO=OB、AOB=90°で半径AOで、A、Bそれぞれから引いた弧の交点をC、Dとし、それぞれをOと結べば3等分=30°になる。すべての弧の半径を統一すること。これにより点C、O、Bを結ぶと正三角形になる。同様に点A、O、Dも正三角形を作るので、内角は60°であり、AOB=90°との関係から30°に3等分割されていることになる。
  1. 　線分aの両端をA、Bとし、その中点をCとする。Cから垂線を描き、AB=CDとなる点Dを求める。
  2. Dを中心にACの長さをADの延長線上に求め、Eとする。
  3. Aを中心にし、半径AEでABからの中線上にFを求める。
  4. コンパスに線分a=ABをとり、F及びA、Bを中心に弧を描き、交点をそれぞれG、Hとする。
  5. AG、GF、FH、BHを結んで作図終了。ABHFGが求める正五角形。
  1. 　線分aの両端をA、Bとし、それぞれを中心とした半径aの弧を描く。交点をOとする。
  2. Oを中心として半径aの円を描き、A、Bを中心とした弧との交点をC、Dとする。
  3. C、Dを中心として半径aの弧を描き、円Oとの交点をE、Fとする。
  4. ABCDEFが求める正六角形の頂点になる。
  1. 内接する正八角形は正方形の各点をABCDとし、対角線を引きます。
  2. 交点をOとし、半径AO（対角線の1/2）を取り、A、B、C、Dの各点から弧を描く。
  3. 正方形の各辺との交点をE、F、G、H、I、J、K、Lとし、これを結べば正八角形になる。
  1. 線分aの両端をA、Bとし、それぞれを中心に半径aで交点を求めCとする。
  2. 線分ACを6等分し、ABの2等分線上にC7、78、89をとる。
  3. 7、8、9はそれぞれ正7角形、正8角形、正9角形の外接円の中心になる。
  4. 半径A7、A8、A9でそれぞれの中心から円を描き、線分aを円周上に取っていけば求める正多角形を描くことができる。

　＊線分の6等分は上記「線分の等分」参照