物体の高さ・幅及び奥行きを一画面上に表す投影図法で、互いに直角に交わる3直線を基準にその投影、縮尺を定めた投影図を軸測投影図と言う。軸測投影図法には尺度の違いによる下記の3種類の分類がある。
　互いに直角な3つの面が、画面に対して全て等しい斜角の位置になり、3直線が皆、等しい縮尺（寸法）で描かれる投影図を「等角投影図法」という。軸測投影図法の最も代表的な図法である。
　アイソメトリック図法（isometric drawing）から、通称「アイソメ」とも呼ばれている。
　120°（360°÷3）の関係にx、y、zのそれぞれの軸方向を取り、同じ寸法（尺度）で描画できるために素早く描くことが可能である。右図で、立方体の各面は同じ大きさの平行四辺形（頂点は60°/120°）になっている。
　この面の角度で用紙全体に薄く印刷してあるものを方眼紙に対して「斜眼紙」という。

●作図のポイント：
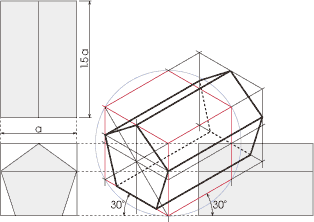
　右図は正五角柱を正投影図（グレーで着色表示）を元に等角投影図法で描いたものである。
　この図法では正面と側面は水平から30°起こした傾きになる。
　寸法を3軸方向にそのまま（同じ尺度で）正投影図から移していくだけで作図ができる。
　またこの図法は消点を持たないので、3軸方向それぞれで平行になるので、30°の傾きを持ったまま、必要な交点を求めていく。
　寸法をそのまま使えることや平行線で描けることなど、複雑な形状でも手際よく表すことができ、ゆがみを多少感じはしても、それなりに立体感を判断できる図法である。

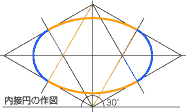
●内接円の作図：
　この図法で水平に配置された正方形は、120°と60°の角度で表されるため、内接円は以下のように作図する。
  1. 上下の120°の頂点を4等分して（各30°）補助線を引く。
  2. 辺との交点までを半径として取り、弧（オレンジ色の線）を描く。
  3. 等分してできた補助線の交点を中心にそれぞれ小さな弧でつなぎ（青線の弧）仕上げる。
楕円テンプレート：
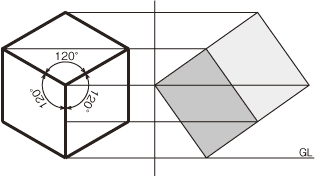
　等角投影図法では大きさに違いはあっても同じ角度の楕円になる。そこで専用のテンプレートの＜35.16°＞がある。使う時は直径を合わせて正確に。
　3直線にすべて異なる縮尺（角度）を持たせた投影図法を不等角投影図法（不等測投影図法）という。
　一般的に30°45°60°を組み合わせて使うことが多い。
　2直線の縮尺が共通（3直線のなす角のうち2角が等しい）ものを二等測投影図法または二等角投影図法という。
　複雑な作図をしなければならない割に立体的なゆがみが強く、不等角投影図法とともにあまり使われることがない。