import java.awt.*;
import java.awt.event.*;
import javax.swing.*;
public class GSample05 extends JFrame {
public GSample05() {
setSize( 800, 600 );
setTitle( "プログラムで絵を描こう" );
addWindowListener( new WindowAdapter(){
public void windowClosing( WindowEvent e ) { System.exit( 0 );}
});
GraphicJPanel jp = new GraphicJPanel();
Container cp = getContentPane();
cp.add( jp );
setVisible( true );
}
public static void main( String[] args ) {
JFrame w = new GSample05();
}
public class GraphicJPanel extends JPanel{
public GraphicJPanel() {
setBackground( Color.white );
}
public void paintComponent( Graphics g ) {
double draw_point_x = 400; //描き始めのx座標
double draw_point_y = 100; //描き始めのy座標(画面の下からの距離)
int depth = 10; //再帰の深さ
int length = 140; //初めの幹の長さ
double scale = 0.7; //縮小するスケール
double height = 600.0; //画面の高さ
g.setColor( new Color( 0x3333cc ) );
drawTree( g, draw_point_x, draw_point_y,
length, 90, depth, scale, height );
}
public void drawTree( Graphics g, double xx, double yy,
double leng, double ang, int t, double scale, double height ) {
double angle = 30.0; //枝を回転させる角度
if( 0 < t ) {
//線の終点のx座標を計算
double x = leng * Math.cos( Math.PI / 180 * ang ) + xx;
//線の終点のy座標を計算
double y = leng * Math.sin( Math.PI / 180 * ang ) + yy;
//線を引く
g.drawLine( ( int )xx, ( int )( height - yy ), ( int )x,
( int )( height - y) );
//角度を-angle度回転させて再帰呼び出し
drawTree( g, x, y, leng * scale, ang - angle, t - 1, scale, height );
//角度を+angle度回転させて再帰呼び出し
drawTree( g, x, y, leng * scale, ang + angle, t - 1, scale, height );
} else {
return;
}
}
}
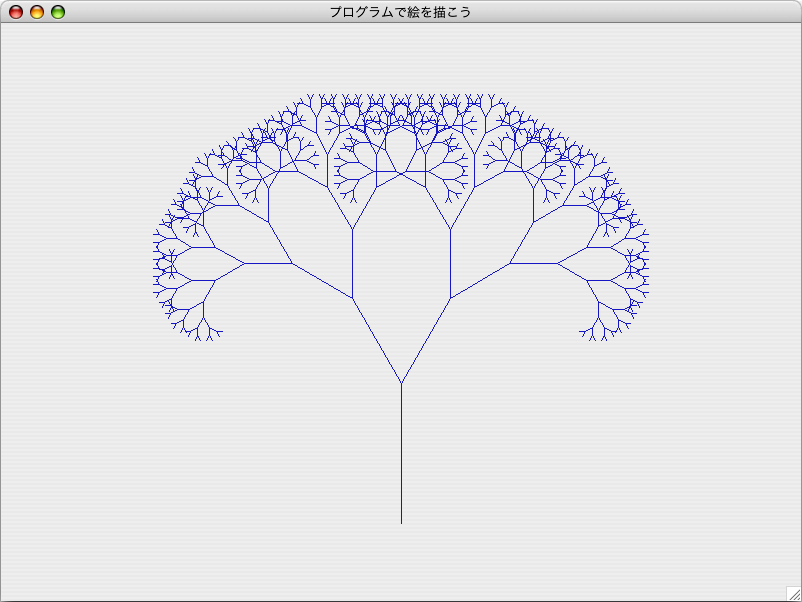
}********************************************************************** GSample05.javaをコンパイルし、実行すると以下のような描画が行われます。 |
import java.awt.*;
import java.awt.event.*;
import javax.swing.*;
public class GSample06 extends JFrame {
public GSample06() {
setSize( 800, 600);
setTitle( "プログラムで絵を描こう" );
addWindowListener( new WindowAdapter(){
public void windowClosing( WindowEvent e ) {
System.exit( 0 );
}
});
GraphicJPanel jp = new GraphicJPanel();
Container cp = getContentPane();
cp.add( jp );
setVisible( true );
}
public static void main( String[] args ) {
JFrame w = new GSample06();
}
public class GraphicJPanel extends JPanel{
public GraphicJPanel() {
setBackground( Color.white );
}
public void paintComponent( Graphics g ) {
double y_point;
double x_point;
double x1_point = 100;
double x2_point = 700;
double y1_point = 100;
double y2_point = 500;
int count = 0;
double rradius = 100;
double rscale = 0.4;
int rtimes = 3;
int step = 10;
for( x_point = x1_point; x_point <= x2_point;
x_point += ( x2_point - x1_point ) / step ) {
y_point = ( ( ( y2_point - y1_point ) /
( x2_point - x1_point ) ) * ( x_point - x1_point ) )
+ y1_point;
if( count % 2 == 1 ) {
g.setColor( new Color( 0x009933 ) );
drawSubOval( g, x_point, y_point,
rradius, rradius, rscale, rtimes );
} else {
g.setColor( new Color( 0xff0033 ) );
drawSubOval( g, x_point, y_point,
rradius / 2, rradius / 2, rscale, rtimes );
}
count++;
}
}
public void drawSubOval( Graphics g, double x, double y,
double width, double height, double scale, int times ) {
double tmp_width = width / 2;
double tmp_height = height / 2;
if( 0 < times ) {
g.drawOval( ( int )( x - width / 2 ), ( int )( y - height / 2 ),
( int )width, ( int )height);
drawSubOval( g, x - tmp_width, y,
width * scale, height * scale, scale, times - 1);
drawSubOval( g, x, y - tmp_height,
width * scale, height * scale, scale, times - 1);
drawSubOval( g, x + tmp_width, y,
width * scale, height * scale, scale, times - 1);
drawSubOval( g, x, y + tmp_height,
width * scale, height * scale, scale, times - 1);
}
}
}
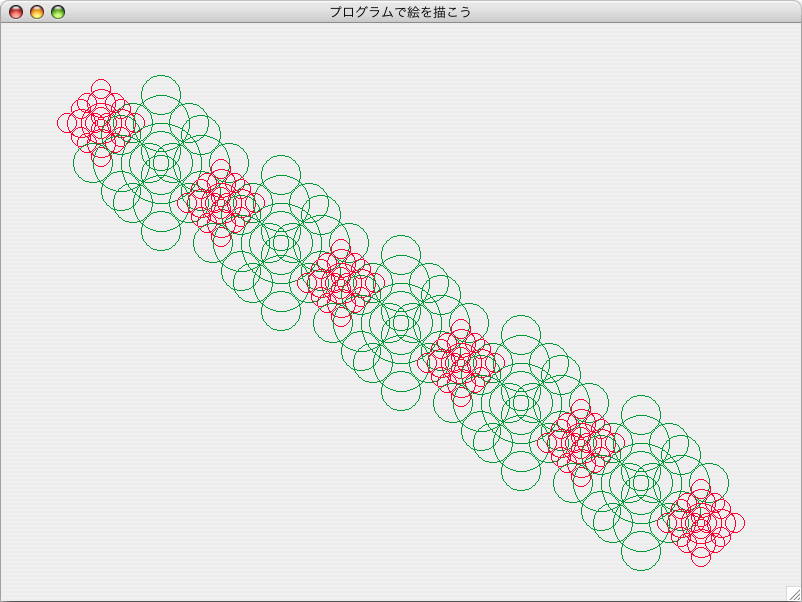
}********************************************************************** GSample06.javaをコンパイルし、実行すると以下のような描画が行われます。 |

|